物体には柔らかさや硬さがあります。ゴムボールと鉄球ではそれぞれはね返り方は変わりますが、これは物理的にどのような意味を持つのでしょうか?
本記事では物体のはね返りやすさを考える重要な概念、反発係数について一緒に勉強していきましょう。
※本記事は運動量およびに運動量保存の法則についての知識を使いますので、ニガテという方はまず下記の2記事を読まれることをお勧めします。
【関連記事】
その1:運動量と力積わかりやすく解説してみた
その2:運動量保存の法則わかりやすく解説してみた
目次
物体の衝突は材質で変わる?
物体同士が衝突をするとき、それぞれの物体の運動の激しさを表す物理量を運動量と呼び、この運動量の総和が一定に保たれることを運動量保存の法則と呼びます。運動量は物体の質量![]() と速度
と速度![]() の積で表され、運動量保存の法則はそれらの和が常に一定になるということです。
の積で表され、運動量保存の法則はそれらの和が常に一定になるということです。
ここで一つ疑問が浮かびます。
もしこの疑問に気づいているならあなたは物理センスのある人なのですが、何かわかりますか?それは「運動の激しさは本当に質量と速度だけで決まるのか?」ということ。
質量が大きく、速度が速い物体ほどその運動が激しくなるであろうというのは、なんとなく理解できると思います。
自転車よりもダンプカーの方が事故が起きた時に悲惨ですし、素人の投げるボールよりプロ野球選手が本気で投げるボールの方が当たると危ないのも理解できるでしょう。

ゴムボールと鉄球のぶつかり方は違う
ですが、仮に同じ質量のゴムボールと鉄球を壁に投げてぶつけた時、その衝突の激しさは同じでしょうか?違いますよね。おそらくゴムボールはポーンとはね返るようにぶつかりますが、鉄球はドスっと鈍い音を鳴らして落ちるはずです。
実は、運動量保存の法則は質量と速度については考えられているのですが「物体の材質」については考慮をしていません。ゴムボールと鉄球の衝突が同じわけはありませんし、質量と速度だけで衝突の激しさが決まるのであればエアーバッグなどは意味をなさないはずです。
物体の衝突を考えるときの要素として質量と速度で決まる運動量の他に「物体のはね返りやすさ」を考えるために編み出されたのが、反発係数 (はね返り係数)です。
反発係数(はね返り係数)とは?
物体が他の物体と衝突した時、その物体のはね返りやすさを表すものを反発係数またははね返り係数と呼びます。(反発係数、はね返り係数どちらで呼んでも良いのですが、本記事では反発係数で統一します)
反発係数の定義はこちら。
速度![]() で移動するある物体が、静止する壁や床にぶつかって速度
で移動するある物体が、静止する壁や床にぶつかって速度![]() に変化した時、ぶつかる前後の速度の比を反発係数(はね返り係数)と呼ぶ。反発係数は通常
に変化した時、ぶつかる前後の速度の比を反発係数(はね返り係数)と呼ぶ。反発係数は通常![]() で表される。
で表される。
反発係数:![]()
反発係数にマイナスがついているのは、跳ね返った前後で通常は速度の向きが逆になることを見越しており、![]() を正の値にするためにつけられています。
を正の値にするためにつけられています。
物体の反発係数![]() が与えられている時、衝突する前または後の速度がわかっていれば反発係数の式を変形することでもう一方の速度を求めることもできます。
が与えられている時、衝突する前または後の速度がわかっていれば反発係数の式を変形することでもう一方の速度を求めることもできます。
反発係数eが与えられているとき
衝突する前の速度:![]()
衝突した後の速度:![]()
反発係数の便利な点は、その値によって物体の衝突を大きく3つに分けることができるということです。
①完全弾性衝突(e=1)
反発係数![]() が1になる時、物体の衝突前後の速さは同じ大きさのままです。
が1になる時、物体の衝突前後の速さは同じ大きさのままです。![]() が成立するときの衝突を完全弾性衝突(弾性衝突)と呼びます。完全弾性衝突では物体の速度の向きが変わるだけでその勢いが衰えることはありません。
が成立するときの衝突を完全弾性衝突(弾性衝突)と呼びます。完全弾性衝突では物体の速度の向きが変わるだけでその勢いが衰えることはありません。
②非弾性衝突(e<1)
完全弾性衝突の場合その前後の速さは変化しませんが、現実世界では壁との摩擦や空気抵抗によって物体の運動量は徐々に消費されてきますので完全弾性衝突は実際に起こることはありません。通常は衝突の後の方が物体の速さは小さくなるため、反発係数![]() は1より小さい値になります。
は1より小さい値になります。
反発係数![]() が成立するときの衝突を非弾性衝突と呼びます。
が成立するときの衝突を非弾性衝突と呼びます。
③完全非弾性衝突(e=0)
最後に全く跳ね返らずに壁にくっついてしまった場合はどうでしょう?
この場合は衝突後の物体の速さが0になるため反発係数![]() となり、このときの衝突を完全非弾性衝突と呼びます。
となり、このときの衝突を完全非弾性衝突と呼びます。
斜めに衝突した場合の反発係数
今までは物体が壁や床に垂直にぶつかった場合の話をしてきましたが、現実の世界では速度は向きを持つので床に斜めにぶつかる場合がほとんどです。床に斜めにぶつかった場合の衝突は、衝突前後の速度を水平方向と鉛直方向に分解することで考えることができます。

面に斜めに衝突した場合
画像のように摩擦の無視できるなめらかな床に対して物体が斜めに衝突したとき、物体の衝突前の鉛直方向の速度と水平方向の速度を![]() と
と![]() 、衝突後の速度をそれぞれ
、衝突後の速度をそれぞれ![]() と
と![]() としましょう。
としましょう。
物体の反発係数を![]() としたとき、水平方向の衝突では床が物体に与える力はありませんので速度は変化しません。
としたとき、水平方向の衝突では床が物体に与える力はありませんので速度は変化しません。
垂直方向の場合は反発係数を使うことで衝突後の速度を表すことができますから、物体の水平方向と鉛直方向の衝突後の速度は以下のように表すことができますね。
水平方向の衝突後の速度:![]()
鉛直方向の衝突後の速度:![]()
2つの物体が衝突した場合の反発係数
壁や床などの静止した面に衝突する場合を考えてきましたが、では衝突する2つの物体がそれぞれ速度を持っている場合はどうでしょうか?この時に役立つのが相対速度です。
相対速度は一方の物体から見たもう一方の速度になるので、片方が静止した場合と同じように反発係数の式を当てはめることができます。移動する物体のそれぞれの速度を![]() 、
、![]() 、衝突後の速度を
、衝突後の速度を![]() 、
、![]() とすると、反発係数は以下の式で表すことができます。
とすると、反発係数は以下の式で表すことができます。
![]()
まとめ
- 物体同士がぶつかる前後の速度の比を反発係数(はね返り係数)と呼ぶ。
- e=1の時の衝突を完全弾性衝突と呼ぶ
- e<1の時の衝突を非弾性衝突と呼ぶ
- e=0の時の衝突を完全非弾性衝突と呼ぶ
では、ここまで読んでいただきありがとうございました。


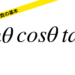








同じ素材同士が衝突したとき、一方は傷つき、一方は傷つかない時があるのは何故か?という疑問のアンサーを探していたら辿り着いた者です。(見た目を重視しており、分子的にはあまり考えていません。日常のふとした時に起こった疑問です。)
物体の衝突は材質で変わる?のゴムボールと鉄球についてですが、質量を同じにするので鉄球の何倍、何十倍も大きくなりますよね?ゴムボールは、)
エアーバックにたどり着くまで衝突エネルギーはバンパーで跳ね返され、車で分散され、座席シートで吸収されますよね?