この記事では電磁気学の「交流」についてわかりやすく解説をしてきます。
交流は電磁気学の総まとめになる分野ですが、難しい言葉が出てくるためとっつきにくく感じている受験生が多いです。
ですが大抵の場合「難しいと思い込んでいる」場合がほとんです。今までの単元と比べて覚えるべき量が少なく、解法のパターンもそこまで多くないので、逆に得点源にしやすい単元です。むしろ苦手な人が多い分、得意にしてしまえば他の受験生との差がつけやすい単元と言えるでしょう。
- これから物理を学ぶ高校生
- 物理を得点源にしたい受験生
に向けて、できるだけ噛み砕いて解説しますので、最後までしっかり読んで理解しましょう!
目次
電磁誘導を利用して発電するには?
コイルを貫く磁束が変化すると、電磁誘導によってコイルに誘導起電力が発生して電流が流れます。
この原理を利用して発電機を作ることができそうですが、一点問題があります。それはコイルが誘導起電力を持ち続けるためには、コイルを貫く磁束を常に変化させ続けなければならないということです。
例えば図のようなコイルに永久磁石を出し入れして発電する場合、磁石を入れたり出したりすると磁束が強まったり弱まったりするため、誘導起電力の向きが一定になりません。

電磁誘導の誘導起電力は向きが安定しない
やや不便そうですが、逆を言えば誘導起電力の向きが入れ替わっても、コイルの磁束を変化させ続けることができれば、電流を流し続けることができるということです。電池は一度使い切ってしまうと起電力を失いますが、発電機として電流を流し続けることができれば便利ですよね。
そこで考え出されたのが「交流」という考え方です。
交流とは
交流とはどんなものでしょうか?その定義はこちら。
交流とは周期的に電圧と電流が変化する電気のこと
今まで扱ってきた回路は直流と呼ばれ電圧と電流が常に一定の回路でした。ですがここから扱う電気は電圧が周期的に変化し、電圧の変化に伴って電流も変化するというもので、これを交流といいます。
これから交流を抵抗やコンデンサーに流した時にどんな現象が起こるか?について学んでいくのですが、今回はその前に交流の基本について学んでいきましょう。
交流の基本として学ばないといけないのは大きく以下の2つです。
- 交流の式と関連する物理量
- 交流電力の実効値
①交流の式と関連する物理量
まずは交流の式と覚えるべき用語をチェックしていきましょう。
交流の式
交流は電圧と電流が周期的に変化する回路なので、単振動の式と同じようにsinを使って表すことができます。
交流電源の作る電圧と電流は、以下の式で表すことができます。
![]()
![]()
単振動の式そのままですね。交流電源の電圧の時間変化は図のような波のグラフで表すことができます。

交流の電圧のグラフ
![]() と
と![]() を周期的に行ったりきたりを繰り返しています。
を周期的に行ったりきたりを繰り返しています。
位相
位相とは周期的な運動の状態を表す量のことで、![]() の部分のことです。
の部分のことです。
位相と聞くとややこしく感じる人もいると思いますが、「sinやcosの中身」ということが理解できていればOKです。
角周波数
交流の式に含まれる![]() を角周波数と呼びます。等速円運動でいう角速度、単振動でいう角振動数と同じものです。
を角周波数と呼びます。等速円運動でいう角速度、単振動でいう角振動数と同じものです。
周期
交流が1回振動するのにかかる時間を周期![]() と呼びます。これも等速円運動や単振動と同じものです。
と呼びます。これも等速円運動や単振動と同じものです。
周波数
1秒間に交流が振動する回数を周波数![]() と呼びます。単振動で扱う振動数と同じものですね。よって以下の式が成り立ちます。
と呼びます。単振動で扱う振動数と同じものですね。よって以下の式が成り立ちます。
角周波数・周期・周波数それぞれの関係
角周波数と周期の関係は円運動の角速度と周期の関係と同じなので、![]() が成立します。
が成立します。
よって式を変形すると角周波数・周期・周波数それぞれの関係は以下のようになります。
![]()
②交流電力の実効値
交流の式に続いて覚えなければならない交流の基本が実効値です。
実効値とは
実効値とは何か?ですが、その定義はこちらです。
交流の場合、電圧や電流が周期的に変化するため電力も一定の値になりません。sinの式で電圧や電流を表しても不便なので、実効値を使って電圧や電流を表します。
実効値とは「交流電圧や電流を直流(常に一定の電気が流れている)として考えた値」のことで、実効値を使うことで周期的な変化をする交流の電圧や電流を、直流のものとして考えることができ便利です。
実効値を表す時は、電圧(電流)の最大値を![]() で割ってあげます。例えば最大値が141Vの交流電圧は実効値100Vになります。
で割ってあげます。例えば最大値が141Vの交流電圧は実効値100Vになります。
日本の家庭用のコンセントは常に100Vに電圧が設定されていますが、実際のところ141Vが最大値の交流電圧が設定されていて、100Vは実効値として![]() で割られたものということです。
で割られたものということです。
なぜ2の平方根で割ると実効値になる?
電力![]() は
は![]() で表すことができますが、交流電源の電圧と電源をそれぞれ
で表すことができますが、交流電源の電圧と電源をそれぞれ![]() 、
、![]() とすると、Pは以下の式になります。
とすると、Pは以下の式になります。
![]() [/latex]
[/latex]
この式をP-tグラフ化してみると、以下のようになります。

交流電力の平均を取ってみる
P-tグラフの最大値は![]() 、最小値は0のため、電力の平均値は
、最小値は0のため、電力の平均値は![]() になります。
になります。
「交流が常に変化するなら平均値![]() を電力として設定すればいいのでは?」と思うかもしれませんが、前についている
を電力として設定すればいいのでは?」と思うかもしれませんが、前についている![]() が邪魔で直流の電力の式
が邪魔で直流の電力の式![]() の形と微妙に違いますよね。
の形と微妙に違いますよね。
これでは使い勝手が悪いです。できれば直流の式と同じ形で使いたいですよね。
そこで![]() 、
、![]() とし、
とし、![]() と
と![]() を実効値として設定しました。
を実効値として設定しました。
実効値を設定することで
![]()
となるため、直流の式と同じ形になりました。
実効値は、交流を直流と同じように考えるために使い勝手がよくなるように発明された値
変圧器
交流に関連してもう1つ学んでおきたいのが「変圧器」です。変圧器とは簡単にいうと「交流の電圧を自由に変えられる部品」のことなのですが、交流の基本から話が少しそれるので、原理については別記事で詳しく解説します。
変圧器も受験の頻出問題ですから、ぜひ下記の記事をチェックしてみてください。
【合わせて読みたい】
まとめ
最後まで読んでいただきありがとうございました!
交流の基本的な考え方について理解できましたか?
最後に交流の基本についてまとめておきます。
- 交流電圧の式:

- 交流電流の式:

- 実効値とは交流を直流と同じように考えるために使い勝手がよくなるように発明された値で、最大値を
 で割ったもの
で割ったもの

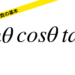







V=I_{0}*sin{ωt}となっています。
I=I_{0}*sin{ωt}ではないでしょうか。